

In the theory of statistics & probability, the below formulas are used in Z-test to estimate Z-statistic (Z 0), critical value (Z e) & null hypothesis test (H 0) to conduct the test of significance for mean, difference between two means, proportion & difference between two proportions. Examples of specific statistical tests will be covered in future reviews. The P-value (probability value) is a quantitative parameter used in statistical hypothesis testing to determine whether a null hypothesis (or claimed hypothesis) is true, or in other words, whether the obtained test results are significant.

Guidelines for the interpretation of P values are also provided in the context of a published example, along with some of the common pitfalls. Evaluate Null Hypothesis: We calculate the standard error of the mean, then calculate Z for each experiment, and then look up the P value for the obtained Z. The sample values should be large enough or approximately equal to the population parameters and all the sampling distributions follow normal asymptotically to conduct the test of significance for large samples using z-test. The present review introduces the general philosophy behind hypothesis (significance) testing and calculation of P values. The probability is smaller for the hypothesized value for mean or proportion to be correct, if the difference between the hypothesized & actual value is higher. From that, since the population parameter we care about is a population mean, she would calculate the sample mean in order to estimate that and the sample standard deviation. The probability is higher for the hypothesized value for mean or proportion to be correct, if the difference between the hypothesized & actual value is smaller. She wants to test her null hypothesis so she takes a sample of size six. Z-statistic is applicable for the test of significance for proportion, difference between two proportions, mean or difference between two means. Here the difference between the hypothesized & actual value of the sample data is being analyzed to determine if the difference is significant or not. The Z-statistic (Z 0) value used to test the validity of assumptions in the test of significance.
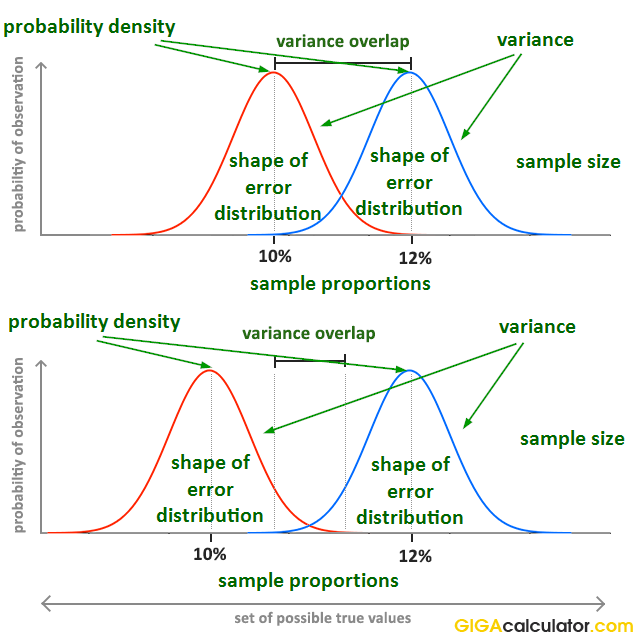
If the p-value is greater than the level of significance, do not reject the null hypothesis. Formally, the p-value is the probability that the test statistic will produce values at least as extreme as the value it produced for your sample.It is crucial to remember that this probability is calculated under the assumption that the null hypothesis is true. If the p-value is less than or equal to the level of signifance, reject the null hypothesis. Because our p-value (0.002221) is less than the standard significance level of 0.05, we can reject the null hypothesis. Z-test is the statistical technique which represents how many standard deviation or standard error the sample mean or proportion (p value) is away from the population mean or success proportions (p value) to check if the test of hypothesis (significance) is accepted in statistical experiments. To test the hypothesis in the p-value approach, compare the p-value to the level of significance.


 0 kommentar(er)
0 kommentar(er)
